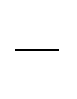Projective Set
Set (see the rules) is the game of finding lines in $\mathbb F_3^4$. Projective Set is the game of finding 2-dimensional subspaces in $\mathbb F_2^6$, or if you prefer, the game of finding lines in $\mathbb P^5_{\mathbb F_2}$.
Set is fun because any line in $\mathbb F_3^4$ contains three points, so any two cards (i.e. points in $\mathbb F_3^4$) uniquely determine a third. I realized that since the same is true in $\mathbb P^5_{\mathbb F_2}$, projective set would also be a fun game.
The Cards
There are six possible features a card can have: a squiggle, beak, ear, vertical, horizontal, and smile:
Any given card must have at least one of these (i.e. must correspond to a nonzero element of $\mathbb F_2^6$), but can otherwise have any combination of them. There are therefore 63 cards in a complete deck of projective set.
To get your own deck of projective set, print out this pdf on some cardstock and cut out the cards. Or use the smaller deck of 31 cards. I recommend cutting off the corners as shown to make it easy to orient all the cards properly.
The Rules
Three cards form a set if two of them XOR to the third. Another way to put it is that three cards form a set if for any given property, either none of the cards have it, or exactly two of them have it. Here are some examples of sets. Note that if three cards form a set, any two of them XOR to the other. Note also that given any two cards, there is a unique third card that will form a set with those two.
Here are some examples of non-sets.
Play
Play is essentially the same as for the game Set.
The dealer shuffles the cards and lays 12 cards (in a rectangle) face up on the table so that they can be seen by all players. The players remove a "set" of three cards as they are seen. Each "set" is checked by the other players. If correct, the "set" is kept by the player and the dealer replaces the three cards with cards from the deck. Players do not take turns but pick up "sets" as soon as they see them. A player must call "set" before picking up the cards. After a player has called "set", no other player can pick up cards until the first player is finished. If a player calls "set" and does not have one, the player loses one point. The three cards are returned to the table.
If all players agree that there is no "set" in the cards showing, three more cards (making a total of 15) are laid face up. These cards are not replaced when the next "set" is picked up, reducing the number to 12 again.
The play continues until the deck is depleted. At the end of the play there may be some cards which do not include a "set".
The number of "sets" held by each player are then counted, one point is given for each and added to their score. The deal then passes to the person on the dealer's left and the play resumes with the deck being reshuffled.
When all players have dealt, the game ends; the highest score wins.
Questions
Are there more games like this?
This paper of Davis and Maclagan claims on page 18 that Set and Projective Set are the only two "abstract SET games".
How many cards can there be without a set?
Also answered on page 18 of the Davis and Maclagan paper. The maximum number of projective set cards without a set is $2^d$, where you're using a deck of $2^{d+1}-1$. (You can easily realize this by picking a property (e.g. squiggle) and taking all the cards which have that property.)
Are there always cards left over at the end?
No. If you play with a deck of size $2^{d+1}-1$ where $d$ is odd, it is possible to break the deck up into disjoint sets. I thought about this problem with Dori Bejleri for a bit. Dori's friend Ryan Thorngren came up with a nice proof.
First note that $\mathbb P^1_{\mathbb F_2}$ can be covered by disjoint lines since it is a single line. Now we induct on dimension. Suppose $\{(a_{i,1},a_{i,2},a_{i,3})\}_i$ is a collection of triples of points in $\mathbb P^{2n-1}_{\mathbb F_2}$ so that each point appears in exactly one triple, and each triple forms a line. Then we have the following decomposition of $\mathbb P^{2n+1}_{\mathbb F_2}$ into lines (in standard projective notation):
- $([0:\cdots:0:0:1], [0:\cdots:0:1:0], [0:\cdots:0:1:1])$
- $([a_{i,1}:0:0], [a_{i,2}:0:0], [a_{i,3}:0:0])$ for each $i$
- $([a_{i,1}:0:1], [a_{i,2}:1:0], [a_{i,3}:1:1])$ for each $i$
I don't like your cards
I generated them with LaTeX as follows. Tweak to taste.
\documentclass{article}
\usepackage[paperwidth=8.5in,paperheight=11in,margin=0in]{geometry}
\usepackage{tikz}
\begin{document}
\thispagestyle{empty}\pagestyle{empty}
\newif\ifone \onetrue
\newif\iftwo \twotrue
\newif\ifthree \threetrue
\newif\iffour \fourtrue
\newif\iffive \fivetrue
\newif\ifsix \sixtrue
\newlength{\x}
\setlength{\x}{.07\textwidth}
\newcommand{\s}{\parbox{.25\textwidth}{\begin{tikzpicture}[line width=1.5mm,scale=1]
\draw[help lines] (-.125\textwidth,-.125\textheight) rectangle (.125\textwidth,.125\textheight);
\clip (-.125\textwidth,-.125\textheight) rectangle (.125\textwidth,.125\textheight);
\ifone \draw (-\x,0) -- (\x,0); \fi
\iftwo \draw (-.05\x,-\x) -- (.05\x,-.6\x) -- (-.05\x,-.2\x) -- (.05\x,.2\x) -- (-.05\x,.6\x) -- (.05\x,\x); \fi
\ifthree \draw (-.5\x,\x) -- (-1.3\x,0) -- (-.5\x,-\x); \fi
\iffour \draw (-.9397\x,-\x) arc (200:340:\x); \fi
\iffive \draw (-\x,1.5\x) .. controls +(0,1\x) and +(0,-1\x) .. (\x,1.5\x); \fi
\ifsix \draw (\x,.8\x) .. controls +(.5\x,\x) and +(.5\x,-1.4\x) .. (\x,-.6\x); \fi
\end{tikzpicture}}
\ifone \onefalse \else
\iftwo \twofalse \onetrue \else
\ifthree \threefalse \twotrue \onetrue \else
\iffour \fourfalse \threetrue \twotrue \onetrue \else
\iffive \fivefalse \fourtrue \threetrue \twotrue \onetrue \else
\sixfalse \fivetrue \fourtrue \threetrue \twotrue \onetrue
\fi
\fi
\fi
\fi
\fi
\hspace{-1mm}}
\newlength{\y}\setlength{\y}{-.5mm}
\noindent
\s\s\s\s \vspace{\y}
\s\s\s\s \vspace{\y}
\s\s\s\s \vspace{\y}
\s\s\s\s \vspace{\y}
\noindent
\s\s\s\s \vspace{\y}
\s\s\s\s \vspace{\y}
\s\s\s\s \vspace{\y}
\s\s\s\s \vspace{\y}
\noindent
\s\s\s\s \vspace{\y}
\s\s\s\s \vspace{\y}
\s\s\s\s \vspace{\y}
\s\s\s\s \vspace{\y}
\noindent
\s\s\s\s \vspace{\y}
\s\s\s\s \vspace{\y}
\s\s\s\s \vspace{\y}
\s\s\s\s \vspace{\y}
\end{document}